Single Cell Dimensional Reduction: Phate

May 25, 2025 · 22 min read · code single cell dimensional reduction phate ·

Following my previous post on t-SNE vs UMAP, I will now check another dimensional reduction technique, PHATE (Potential of Heat-diffusion for Affinity-based Transition Embedding). According to the authors PHATE is a visualization method that captures both local and global nonlinear structure using an information-geometric distance between data points.

For this test I will compare PHATE vs UMAP using two of the datasets used in the tutorials, embriod body differentiation & bone marrow, plus the pancreas dataset used in the pseudotime trajectory and RNA velocity posts.

PHATE is implemented in Python and R (and MATLAB!). However, the R implementation uses reticulate to access the Python package so I will directly use the Python implementation. I run the code in Jupyter Notebook to work in a more interactive environment.

Embriod Body differentiation

The Embriod Body (EB) dataset is publically available as scRNAseq.zip at Mendelay Datasets at https://data.mendeley.com/datasets/v6n743h5ng/. This analysis is partially based on the PHATE tutorial

import packages

1import os
2import scprep
3import pandas as pd
4import numpy as np
5import phate

import data using scprep

1sparse=True
2T1 = scprep.io.load_10X(os.path.join("scRNAseq", "T0_1A"), sparse=sparse, gene_labels='both')
3T2 = scprep.io.load_10X(os.path.join("scRNAseq", "T2_3B"), sparse=sparse, gene_labels='both')
4T3 = scprep.io.load_10X(os.path.join("scRNAseq", "T4_5C"), sparse=sparse, gene_labels='both')
5T4 = scprep.io.load_10X(os.path.join("scRNAseq", "T6_7D"), sparse=sparse, gene_labels='both')
6T5 = scprep.io.load_10X(os.path.join("scRNAseq", "T8_9E"), sparse=sparse, gene_labels='both')

check the data

1T1

	RP11-34P13.3 (ENSG00000243485)	FAM138A (ENSG00000237613)	OR4F5 (ENSG00000186092)	RP11-34P13.7 (ENSG00000238009)	RP11-34P13.8 (ENSG00000239945)	RP11-34P13.14 (ENSG00000239906)	RP11-34P13.9 (ENSG00000241599)	FO538757.3 (ENSG00000279928)	FO538757.2 (ENSG00000279457)	AP006222.2 (ENSG00000228463)	...	AC007325.2 (ENSG00000277196)	BX072566.1 (ENSG00000277630)	AL354822.1 (ENSG00000278384)	AC023491.2 (ENSG00000278633)	AC004556.1 (ENSG00000276345)	AC233755.2 (ENSG00000277856)	AC233755.1 (ENSG00000275063)	AC240274.1 (ENSG00000271254)	AC213203.1 (ENSG00000277475)	FAM231B (ENSG00000268674)
0
AAACATACCAGAGG-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
AAACATTGAAAGCA-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
AAACATTGAAGTGA-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
AAACATTGGAGGTG-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
AAACATTGGTTTCT-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
TTTGACTGCTTCTA-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TTTGACTGTGCCCT-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TTTGCATGAGGTCT-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TTTGCATGGGCGAA-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TTTGCATGTGACAC-1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0

4649 rows × 33694 columns

perform preprocessing as described in the Phate tutorial

1filtered_batches = []
2for batch in [T1, T2, T3, T4, T5]:
3    batch = scprep.filter.filter_library_size(batch, percentile=20, keep_cells='above')
4    batch = scprep.filter.filter_library_size(batch, percentile=75, keep_cells='below')
5    filtered_batches.append(batch)
6del T1, T2, T3, T4, T5 # removes objects from memory

Merge all datasets and create a vector representing the time point of each sample

1EBT_counts, sample_labels = scprep.utils.combine_batches(
2    filtered_batches, 
3    ["Day 00-03", "Day 06-09", "Day 12-15", "Day 18-21", "Day 24-27"],
4    append_to_cell_names=True
5)
6del filtered_batches # removes objects from memory
7EBT_counts

	A1BG (ENSG00000121410)	A1BG-AS1 (ENSG00000268895)	A1CF (ENSG00000148584)	A2M (ENSG00000175899)	A2M-AS1 (ENSG00000245105)	A2ML1 (ENSG00000166535)	A2ML1-AS1 (ENSG00000256661)	A2ML1-AS2 (ENSG00000256904)	A3GALT2 (ENSG00000184389)	A4GALT (ENSG00000128274)	...	ZXDC (ENSG00000070476)	ZYG11A (ENSG00000203995)	ZYG11B (ENSG00000162378)	ZYX (ENSG00000159840)	ZZEF1 (ENSG00000074755)	ZZZ3 (ENSG00000036549)	bP-21264C1.2 (ENSG00000278932)	bP-2171C21.3 (ENSG00000279501)	bP-2189O9.3 (ENSG00000279579)	hsa-mir-1253 (ENSG00000272920)
AAACATTGAAAGCA-1_Day 00-03	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
AAACCGTGCAGAAA-1_Day 00-03	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
AAACCGTGGAAGGC-1_Day 00-03	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
AAACGCACCGGTAT-1_Day 00-03	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
AAACGCACCTATTC-1_Day 00-03	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0	0.0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
TTTCTACTCTTATC-1_Day 24-27	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TTTCTACTTGAGCT-1_Day 24-27	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TTTGCATGATGACC-1_Day 24-27	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TTTGCATGCACTCC-1_Day 24-27	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
TTTGCATGTTCTTG-1_Day 24-27	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0	0.0	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0

18691 rows × 33694 columns

Eliminate genes that are expressed in 10 cells or fewer & correct for differences in library sizes. Check mitocondrial content.

1EBT_counts = scprep.filter.filter_rare_genes(EBT_counts, min_cells=10)
2EBT_counts = scprep.normalize.library_size_normalize(EBT_counts)
3mito_genes = scprep.select.get_gene_set(EBT_counts, starts_with="MT-") # Get all mitochondrial genes. There are 14, FYI.
4scprep.plot.plot_gene_set_expression(EBT_counts, genes=mito_genes, percentile=90)

/home/alfonso/.virtualenvs/phate/lib/python3.10/site-packages/scprep/plot/utils.py:104: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
  fig.show()





<Axes: xlabel='Gene expression', ylabel='Number of cells'>

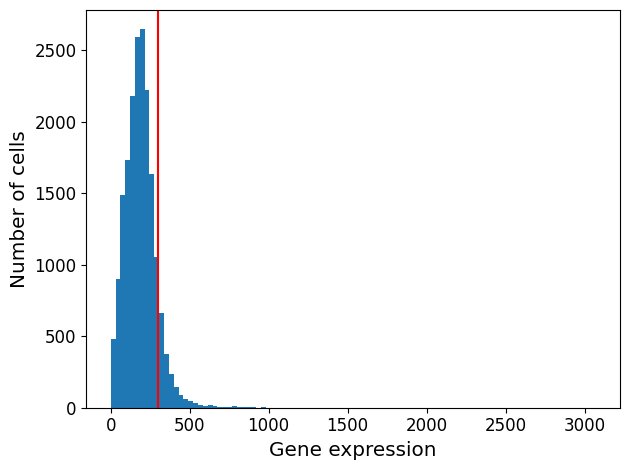
Remove cells with the highest mitochondrial RNA expression levels.

1EBT_counts, sample_labels = scprep.filter.filter_gene_set_expression(
2    EBT_counts, sample_labels, genes=mito_genes, 
3    percentile=90, keep_cells='below')

The tutorial says they use sqrt transformation to avoid adding pseudo-counts during log transformation.

1EBT_counts_sqrt = scprep.transform.sqrt(EBT_counts)

Apply Phate, here are the parameters:

knn : Number of nearest neighbors (default: 5). Increase this (e.g. to 20) if your PHATE embedding appears very disconnected. You should also consider increasing knn if your dataset is extremely large (e.g. >100k cells)
decay : Alpha decay (default: 15). Decreasing decay increases connectivity on the graph, increasing decay decreases connectivity. This rarely needs to be tuned. Set it to None for a k-nearest neighbors kernel.
t : Number of times to power the operator (default: 'auto'). This is equivalent to the amount of smoothing done to the data. It is chosen automatically by default, but you can increase it if your embedding lacks structure, or decrease it if the structure looks too compact.
gamma : Informational distance constant (default: 1). gamma=1 gives the PHATE log potential, but other informational distances can be interesting. If most of the points seem concentrated in one section of the plot, you can try gamma=0.

1phate_operator = phate.PHATE(n_jobs=-2)
2Y_phate = phate_operator.fit_transform(EBT_counts_sqrt)

Calculating PHATE...
  Running PHATE on 16821 observations and 17845 variables.
  Calculating graph and diffusion operator...
    Calculating PCA...
    Calculated PCA in 16.54 seconds.
    Calculating KNN search...
    Calculated KNN search in 7.71 seconds.
    Calculating affinities...
    Calculated affinities in 0.56 seconds.
  Calculated graph and diffusion operator in 25.53 seconds.
  Calculating landmark operator...
    Calculating SVD...
    Calculated SVD in 0.80 seconds.
    Calculating KMeans...
    Calculated KMeans in 2.48 seconds.
  Calculated landmark operator in 3.99 seconds.
  Calculating optimal t...
    Automatically selected t = 19
  Calculated optimal t in 1.60 seconds.
  Calculating diffusion potential...
  Calculated diffusion potential in 0.44 seconds.
  Calculating metric MDS...
  Calculated metric MDS in 3.47 seconds.
Calculated PHATE in 35.05 seconds.

plot results

1scprep.plot.scatter2d(Y_phate, c=sample_labels, figsize=(12,8), cmap="Spectral",
2                      ticks=False, label_prefix="PHATE")

/home/alfonso/.virtualenvs/phate/lib/python3.10/site-packages/scprep/plot/utils.py:104: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
  fig.show()





<Axes: xlabel='PHATE1', ylabel='PHATE2'>

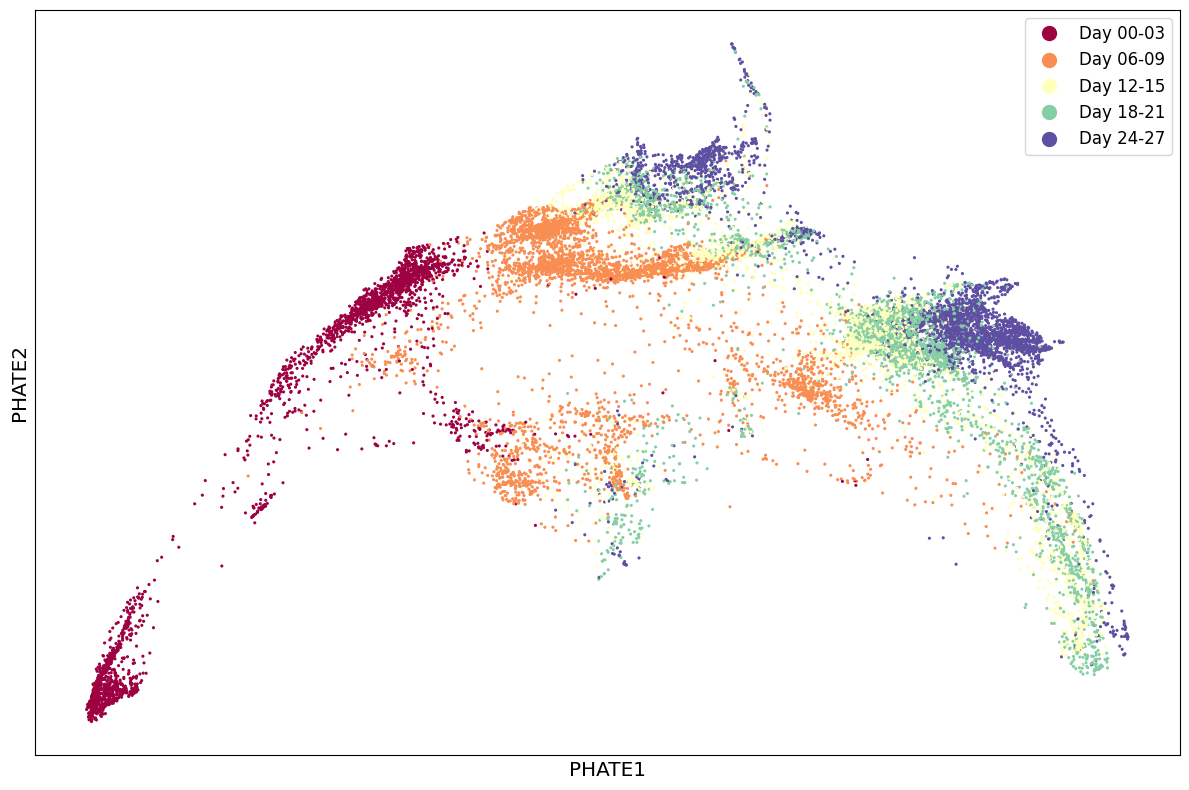
Adjust parameters to the expected sparsity of the trajectories.

1phate_operator.set_params(knn=4, decay=15, t=12)
2# We could also create a new operator:
3# phate_operator = phate.PHATE(knn=4, decay=15, t=12, n_jobs=-2)
4
5Y_phate = phate_operator.fit_transform(EBT_counts_sqrt)

Calculating PHATE...
  Running PHATE on 16821 observations and 17845 variables.
  Calculating graph and diffusion operator...
    Calculating PCA...
    Calculated PCA in 15.63 seconds.
    Calculating KNN search...
    Calculated KNN search in 7.79 seconds.
    Calculating affinities...
    Calculated affinities in 9.19 seconds.
  Calculated graph and diffusion operator in 33.02 seconds.
  Calculating landmark operator...
    Calculating SVD...
    Calculated SVD in 2.34 seconds.
    Calculating KMeans...
    Calculated KMeans in 2.41 seconds.
  Calculated landmark operator in 5.66 seconds.
  Calculating diffusion potential...
  Calculated diffusion potential in 0.24 seconds.
  Calculating metric MDS...
  Calculated metric MDS in 3.72 seconds.
Calculated PHATE in 42.64 seconds.

1scprep.plot.scatter2d(Y_phate, c=sample_labels, figsize=(12,8), cmap="Spectral",
2                      ticks=False, label_prefix="PHATE")

/home/alfonso/.virtualenvs/phate/lib/python3.10/site-packages/scprep/plot/utils.py:104: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
  fig.show()





<Axes: xlabel='PHATE1', ylabel='PHATE2'>

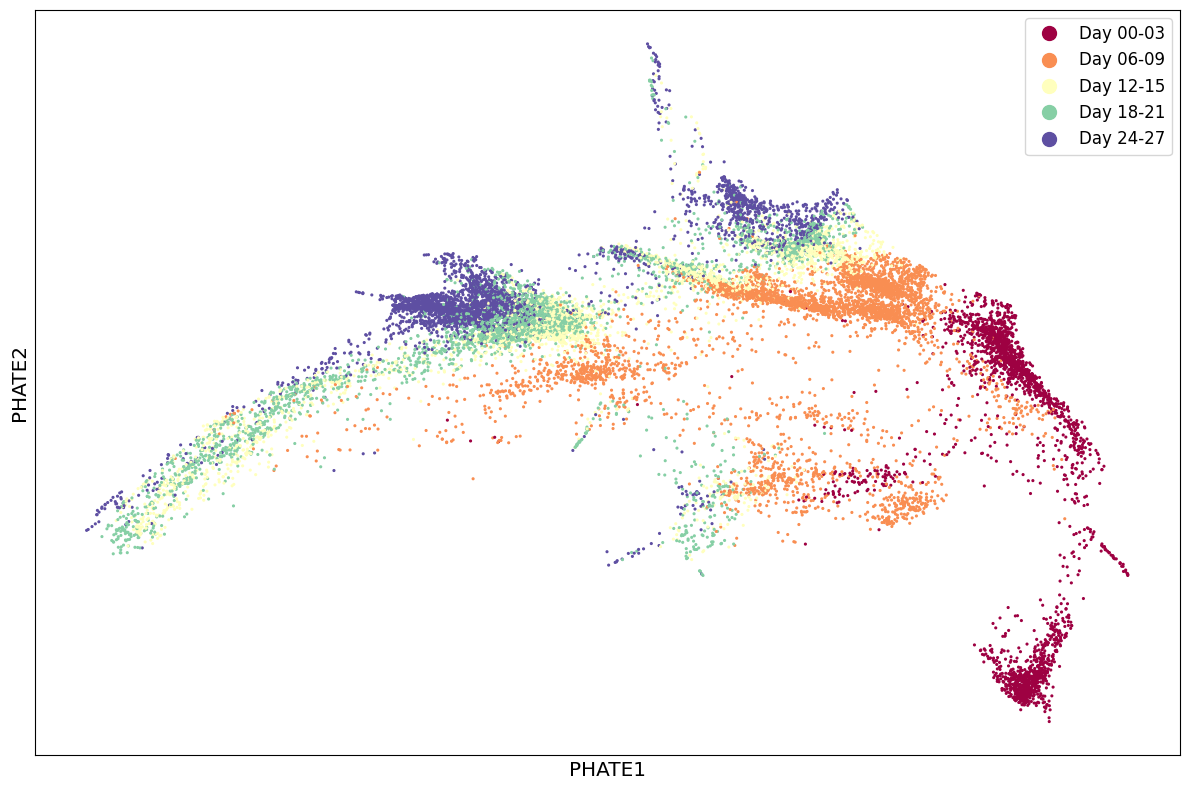
Let's see the results in 3D

1phate_operator.set_params(n_components=3)

PHATE(decay=15, knn=4, n_components=3, n_jobs=-2, t=12)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

1Y_phate_3d = phate_operator.transform()

Calculating metric MDS...
Calculated metric MDS in 33.38 seconds.

1scprep.plot.scatter3d(Y_phate_3d, c=sample_labels, figsize=(8,6), cmap="Spectral",
2                      ticks=False, label_prefix="PHATE")

/home/alfonso/.virtualenvs/phate/lib/python3.10/site-packages/scprep/plot/utils.py:104: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
  fig.show()





<Axes3D: xlabel='PHATE1', ylabel='PHATE2', zlabel='PHATE3'>

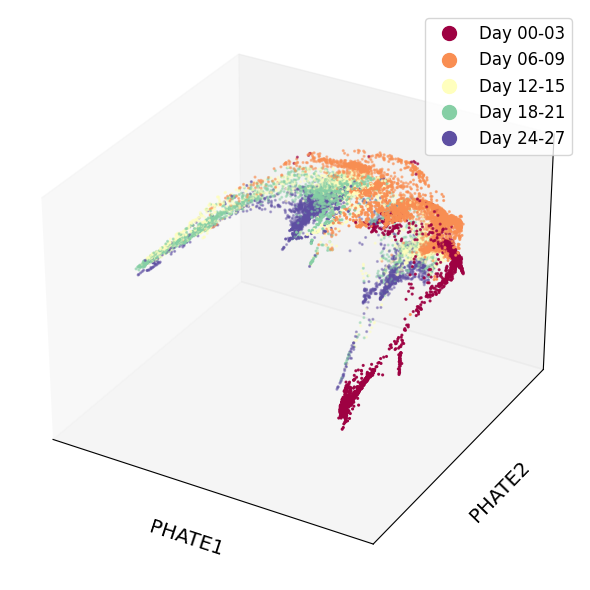
let's create an interactive 3D plot using Plotly

1import numpy as np
2import plotly.express as px
3import plotly.colors
4import pandas as pd
5import plotly.io as pio
6pio.renderers.default = 'notebook'

Create a DataFrame for plotting

1df = pd.DataFrame(Y_phate_3d, columns=['x', 'y', 'z'])
2df['label'] = sample_labels.values
3df

	x	y	z	label
0	0.020654	-0.000396	-0.000804	Day 00-03
1	0.018222	-0.035808	-0.012899	Day 00-03
2	0.020209	-0.036790	-0.011559	Day 00-03
3	0.020340	0.001434	-0.003939	Day 00-03
4	0.019314	-0.038632	-0.014137	Day 00-03
...	...	...	...	...
16816	-0.015878	0.003464	-0.005035	Day 24-27
16817	-0.013085	0.005707	0.001802	Day 24-27
16818	-0.017589	0.001709	-0.005155	Day 24-27
16819	-0.017692	0.001643	-0.005955	Day 24-27
16820	-0.015194	0.004656	-0.003109	Day 24-27

16821 rows × 4 columns

now the plot

 1custom_color_map = {
 2    'Day 00-03': '#9e0142',
 3    'Day 06-09': '#f46d43',
 4    'Day 12-15': '#fdfd9a',
 5    'Day 18-21': '#66c2a5',
 6    'Day 24-27': '#5e4fa2'
 7}
 8
 9fig = px.scatter_3d(
10    df, 
11    x='x', 
12    y='y', 
13    z='z',
14    color='label',
15    color_discrete_map=custom_color_map
16)
17
18fig.update_traces(marker=dict(size=1))
19
20fig.update_layout(
21    legend=dict(
22        itemsizing='constant',
23        font=dict(size=12)
24    ),
25    scene=dict(
26        xaxis=dict(
27            title='PHATE 1',
28            showticklabels=False,
29            showline=True,
30            zeroline=False,
31            linecolor='black',
32            backgroundcolor='rgba(0,0,0,0)',
33            gridcolor='lightgrey',
34            showgrid=True 
35        ),
36        yaxis=dict(
37            title='PHATE 2',
38            showticklabels=False,
39            showline=True,
40            zeroline=False,
41            linecolor='black',
42            backgroundcolor='rgba(0,0,0,0)',
43            gridcolor='lightgrey',
44            showgrid=True
45        ),
46        zaxis=dict(
47            title='PHATE 3',
48            showticklabels=False,
49            showline=True,
50            zeroline=False,
51            linecolor='black',
52            backgroundcolor='rgba(0,0,0,0)',
53            gridcolor='lightgrey',
54            showgrid=True
55        )
56    )
57)
58fig.write_html("../../../static/images/plot1.html", include_plotlyjs="embed")

The only drawback of working with Jupyter notebook is that when I import the notebook to markdown to publish this blog, the interactive plots are not rendered. So I will save the plots as HTML files and link them here. Click here to view the interactive plot

generate UMAP with scanpy

1import anndata as ad
2import scipy.sparse as sp
3import scanpy as sc

1isinstance(sample_labels, pd.DataFrame)

False

start from the same counts before transforming with sqrt

1bdata = ad.AnnData(
2    X=sp.csr_matrix(EBT_counts.values),
3    obs=pd.DataFrame({'sample':sample_labels.values})
4)

/home/alfonso/.virtualenvs/phate/lib/python3.10/site-packages/anndata/_core/aligned_df.py:68: ImplicitModificationWarning:

Transforming to str index.

1bdata.layers["counts"] = bdata.X.copy()
2# Normalizing to median total counts
3# sc.pp.normalize_total(bdata)
4# Logarithmize the data
5sc.pp.log1p(bdata)

1sc.pp.highly_variable_genes(bdata, n_top_genes=2000, batch_key="sample")

/home/alfonso/.virtualenvs/phate/lib/python3.10/site-packages/numba/np/ufunc/parallel.py:371: NumbaWarning:

The TBB threading layer requires TBB version 2021 update 6 or later i.e., TBB_INTERFACE_VERSION >= 12060. Found TBB_INTERFACE_VERSION = 12050. The TBB threading layer is disabled.

1sc.tl.pca(bdata)

1sc.pl.pca(
2    bdata,
3    color="sample"
4)

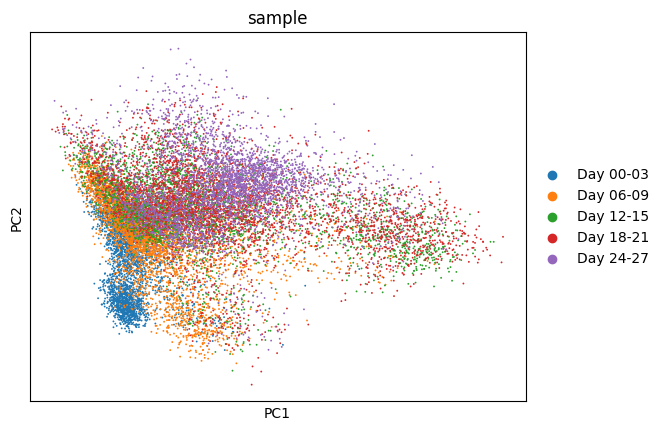
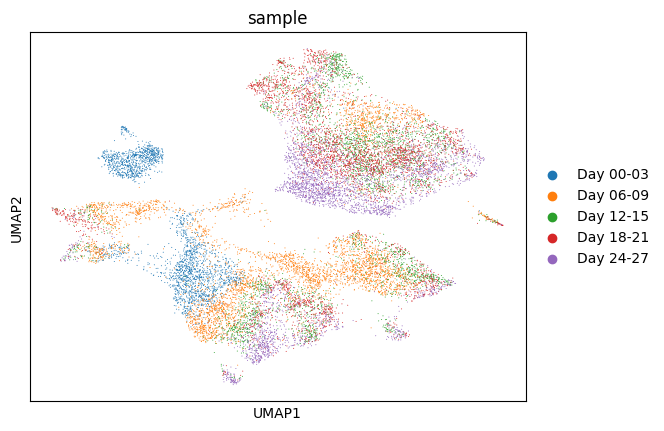
1sc.pp.neighbors(bdata)
2sc.tl.umap(bdata)
3sc.pl.umap(
4    bdata,
5    color="sample",
6    size=2,
7)

/home/alfonso/.virtualenvs/phate/lib/python3.10/site-packages/tqdm/auto.py:21: TqdmWarning:

IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html

1sc.tl.umap(bdata, n_components=3, key_added='UMAP_3D')

1df2 = pd.DataFrame(bdata.obsm['UMAP_3D'], columns=['x', 'y', 'z'])
2df2['label'] = bdata.obs['sample'].values

 1# Create the 3D scatter plot
 2fig = px.scatter_3d(
 3    df2, 
 4    x='x', 
 5    y='y', 
 6    z='z',
 7    color='label',
 8    color_discrete_map=custom_color_map
 9)
10
11fig.update_traces(marker=dict(size=1))
12
13fig.update_layout(
14    legend=dict(
15        itemsizing='constant',
16        font=dict(size=12)
17    ),
18    scene=dict(
19        xaxis=dict(
20            title='UMAP 1',
21            showticklabels=False,
22            showline=True,
23            zeroline=False,
24            linecolor='black',
25            backgroundcolor='rgba(0,0,0,0)',
26            gridcolor='lightgrey',
27            showgrid=True 
28        ),
29        yaxis=dict(
30            title='UMAP 2',
31            showticklabels=False,
32            showline=True,
33            zeroline=False,
34            linecolor='black',
35            backgroundcolor='rgba(0,0,0,0)',
36            gridcolor='lightgrey',
37            showgrid=True
38        ),
39        zaxis=dict(
40            title='UMAP 3',
41            showticklabels=False,
42            showline=True,
43            zeroline=False,
44            linecolor='black',
45            backgroundcolor='rgba(0,0,0,0)',
46            gridcolor='lightgrey',
47            showgrid=True
48        )
49    )
50)
51
52fig.write_html("../../../static/images/plot2.html", include_plotlyjs="embed")

Click here to view the interactive plot

now with sqrt transformed data

1ddata = ad.AnnData(
2    X=sp.csr_matrix(EBT_counts_sqrt.values),
3    obs=pd.DataFrame({'sample':sample_labels.values})
4)

/home/alfonso/.virtualenvs/phate/lib/python3.10/site-packages/anndata/_core/aligned_df.py:68: ImplicitModificationWarning:

Transforming to str index.

1sc.pp.highly_variable_genes(ddata, n_top_genes=2000, batch_key="sample")
2sc.tl.pca(ddata)
3sc.pl.pca(
4    ddata,
5    color="sample"
6)

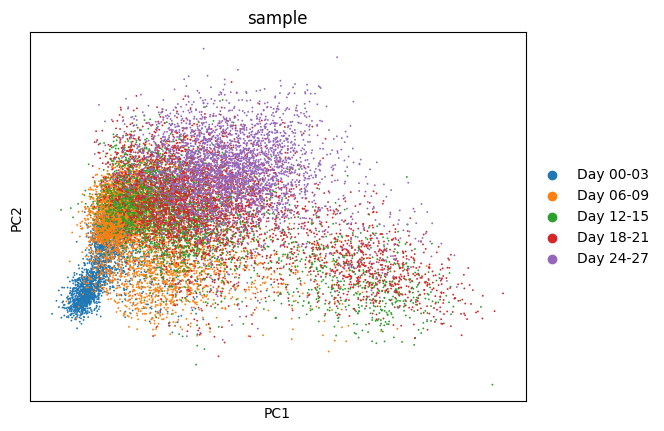
1sc.pp.neighbors(ddata)
2sc.tl.umap(ddata)
3sc.pl.umap(
4    ddata,
5    color="sample",
6    size=2,
7)

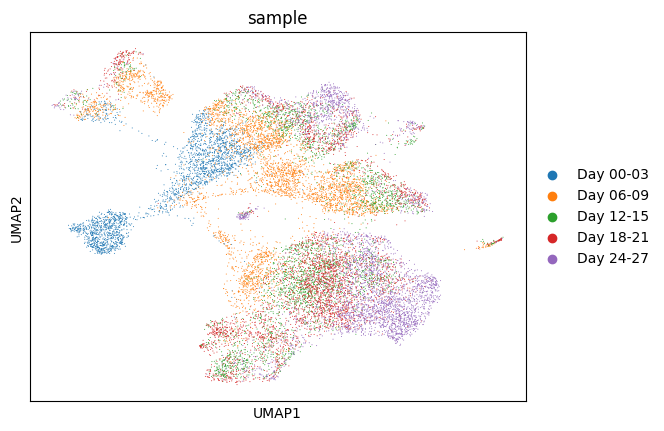
 1sc.tl.umap(ddata, n_components=3, key_added='UMAP_3D')
 2
 3df5 = pd.DataFrame(bdata.obsm['UMAP_3D'], columns=['x', 'y', 'z'])
 4df5['label'] = bdata.obs['sample'].values
 5
 6fig = px.scatter_3d(
 7    df5, 
 8    x='x', 
 9    y='y', 
10    z='z',
11    color='label',
12    color_discrete_map=custom_color_map
13)
14
15fig.update_traces(marker=dict(size=1))
16
17fig.update_layout(
18    legend=dict(
19        itemsizing='constant',
20        font=dict(size=12)
21    ),
22    scene=dict(
23        xaxis=dict(
24            title='UMAP 1',
25            showticklabels=False,
26            showline=True,
27            zeroline=False,
28            linecolor='black',
29            backgroundcolor='rgba(0,0,0,0)',
30            gridcolor='lightgrey',
31            showgrid=True 
32        ),
33        yaxis=dict(
34            title='UMAP 2',
35            showticklabels=False,
36            showline=True,
37            zeroline=False,
38            linecolor='black',
39            backgroundcolor='rgba(0,0,0,0)',
40            gridcolor='lightgrey',
41            showgrid=True
42        ),
43        zaxis=dict(
44            title='UMAP 3',
45            showticklabels=False,
46            showline=True,
47            zeroline=False,
48            linecolor='black',
49            backgroundcolor='rgba(0,0,0,0)',
50            gridcolor='lightgrey',
51            showgrid=True
52        )
53    )
54)
55fig.write_html("../../../static/images/plot3.html", include_plotlyjs="embed")

Click here to view the interactive plot

The shape of the PHATE and UMAP plots are very different. However, when we look at the relationship among the different cell types the biological conclusions would be similar. Specially in the 3D versions.

There is no clear difference between the sqrt transformed and the log transformed data for the UMAP embeddings.

Bone Marrow

For the bone marrow dataset, I adapted this R tutorial and manually downloaded the BMMC myeloid dataset.

Load and check the data

1file.gz = "BMMC_myeloid.csv.gz"
2bmmsc = pd.read_csv(file.gz, compression='gzip', index_col=0)
3bmmsc

	0610007C21Rik;Apr3	0610007L01Rik	0610007P08Rik;Rad26l	0610007P14Rik	0610007P22Rik	0610008F07Rik	0610009B22Rik	0610009D07Rik	0610009O20Rik	0610010B08Rik;Gm14434;Gm14308	...	mTPK1;Tpk1	mimp3;Igf2bp3;AK045244	mszf84;Gm14288;Gm14435;Gm8898	mt-Nd4	mt3-mmp;Mmp16	rp9	scmh1;Scmh1	slc43a2;Slc43a2	tsec-1;Tex9	tspan-3;Tspan3
W31105	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	2	0	0	0	0
W31106	0	0	0	1	0	0	0	0	0	0	...	0	0	0	0	0	1	1	0	0	0
W31107	0	1	0	2	0	0	0	0	0	0	...	0	0	0	0	0	3	1	0	0	2
W31108	0	1	0	1	0	0	0	0	0	0	...	0	0	0	0	0	3	1	0	0	0
W31109	0	0	1	0	0	0	0	1	3	0	...	0	0	0	0	0	5	0	0	0	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
W39164	0	0	1	0	0	0	0	0	0	0	...	0	0	0	0	0	4	0	0	0	0
W39165	1	0	0	1	0	0	0	0	0	0	...	0	0	0	0	0	1	0	0	0	0
W39166	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
W39167	1	3	0	0	0	0	0	0	0	0	...	0	0	0	0	0	1	0	0	0	0
W39168	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	1	1	1	0	1

2730 rows × 27297 columns

Filter to keep genes expressed in at least 10 cells

1keep_cols = (bmmsc > 0).sum(axis=0) > 10
2bmmsc = bmmsc.loc[:, keep_cols]

compute library sizes (total UMIs per cell) and visualize using a histogram

 1import matplotlib.pyplot as plt
 2
 3library_sizes = bmmsc.sum(axis=1)
 4
 5plt.figure(figsize=(8, 5))
 6plt.hist(library_sizes, bins=50, color='skyblue', edgecolor='skyblue')
 7plt.axvline(x=1000, color='red', linestyle='-')
 8plt.xlabel('Total UMIs per cell')
 9plt.ylabel('Number of cells')
10plt.title('Library Size Distribution')
11plt.tight_layout()
12plt.show()

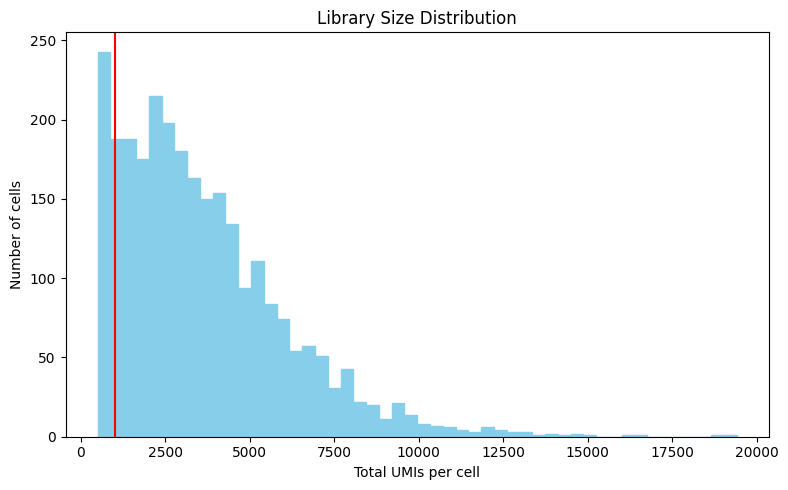
Keep cells with at least 1000 UMIs

1
2keep_rows = library_sizes > 1000
3bmmsc = bmmsc.loc[keep_rows, :]
4bmmsc

	0610007C21Rik;Apr3	0610007L01Rik	0610007P08Rik;Rad26l	0610007P14Rik	0610007P22Rik	0610009B22Rik	0610009D07Rik	0610009O20Rik	0610010F05Rik;mKIAA1841;Kiaa1841	0610010K14Rik;Rnasek	...	mKIAA1632;5430411K18Rik	mKIAA1994;Tsc22d1	mSox5L;Sox5	mTPK1;Tpk1	mimp3;Igf2bp3;AK045244	rp9	scmh1;Scmh1	slc43a2;Slc43a2	tsec-1;Tex9	tspan-3;Tspan3
W31106	0	0	0	1	0	0	0	0	0	1	...	0	0	0	0	0	1	1	0	0	0
W31107	0	1	0	2	0	0	0	0	0	3	...	0	2	0	0	0	3	1	0	0	2
W31108	0	1	0	1	0	0	0	0	0	3	...	0	0	0	0	0	3	1	0	0	0
W31109	0	0	1	0	0	0	1	3	0	8	...	0	5	0	0	0	5	0	0	0	0
W31110	0	1	0	0	0	0	0	1	0	1	...	0	0	0	0	0	3	0	0	0	1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
W39163	0	2	1	0	0	0	0	0	0	1	...	0	0	0	0	0	0	0	0	0	0
W39164	0	0	1	0	0	0	0	0	0	1	...	0	0	0	0	0	4	0	0	0	0
W39165	1	0	0	1	0	0	0	0	0	7	...	2	0	0	0	0	1	0	0	0	0
W39167	1	3	0	0	0	0	0	0	0	3	...	0	0	0	0	0	1	0	0	0	0
W39168	0	0	0	0	0	0	0	0	0	4	...	1	1	0	0	0	1	1	1	0	1

2414 rows × 10738 columns

Normalize the data using library size

1bmmsc_norm = scprep.normalize.library_size_normalize(bmmsc)
2bmmsc_norm

	0610007C21Rik;Apr3	0610007L01Rik	0610007P08Rik;Rad26l	0610007P14Rik	0610007P22Rik	0610009B22Rik	0610009D07Rik	0610009O20Rik	0610010F05Rik;mKIAA1841;Kiaa1841	0610010K14Rik;Rnasek	...	mKIAA1632;5430411K18Rik	mKIAA1994;Tsc22d1	mSox5L;Sox5	mTPK1;Tpk1	mimp3;Igf2bp3;AK045244	rp9	scmh1;Scmh1	slc43a2;Slc43a2	tsec-1;Tex9	tspan-3;Tspan3
W31106	0.000000	0.000000	0.000000	2.480774	0.0	0.0	0.000000	0.000000	0.0	2.480774	...	0.000000	0.000000	0.0	0.0	0.0	2.480774	2.480774	0.000000	0.0	0.000000
W31107	0.000000	1.291823	0.000000	2.583646	0.0	0.0	0.000000	0.000000	0.0	3.875468	...	0.000000	2.583646	0.0	0.0	0.0	3.875468	1.291823	0.000000	0.0	2.583646
W31108	0.000000	1.415629	0.000000	1.415629	0.0	0.0	0.000000	0.000000	0.0	4.246886	...	0.000000	0.000000	0.0	0.0	0.0	4.246886	1.415629	0.000000	0.0	0.000000
W31109	0.000000	0.000000	1.154468	0.000000	0.0	0.0	1.154468	3.463403	0.0	9.235742	...	0.000000	5.772339	0.0	0.0	0.0	5.772339	0.000000	0.000000	0.0	0.000000
W31110	0.000000	4.237288	0.000000	0.000000	0.0	0.0	0.000000	4.237288	0.0	4.237288	...	0.000000	0.000000	0.0	0.0	0.0	12.711864	0.000000	0.000000	0.0	4.237288
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
W39163	0.000000	8.714597	4.357298	0.000000	0.0	0.0	0.000000	0.000000	0.0	4.357298	...	0.000000	0.000000	0.0	0.0	0.0	0.000000	0.000000	0.000000	0.0	0.000000
W39164	0.000000	0.000000	1.249375	0.000000	0.0	0.0	0.000000	0.000000	0.0	1.249375	...	0.000000	0.000000	0.0	0.0	0.0	4.997501	0.000000	0.000000	0.0	0.000000
W39165	1.758087	0.000000	0.000000	1.758087	0.0	0.0	0.000000	0.000000	0.0	12.306610	...	3.516174	0.000000	0.0	0.0	0.0	1.758087	0.000000	0.000000	0.0	0.000000
W39167	1.916810	5.750431	0.000000	0.000000	0.0	0.0	0.000000	0.000000	0.0	5.750431	...	0.000000	0.000000	0.0	0.0	0.0	1.916810	0.000000	0.000000	0.0	0.000000
W39168	0.000000	0.000000	0.000000	0.000000	0.0	0.0	0.000000	0.000000	0.0	3.862122	...	0.965531	0.965531	0.0	0.0	0.0	0.965531	0.965531	0.965531	0.0	0.965531

2414 rows × 10738 columns

Sqrt transformation as before

1bmmsc_norm = scprep.transform.sqrt(bmmsc_norm)

Define PHATE operator and run PHATE

1phate_operator = phate.PHATE(n_jobs=-2)
2Y_phate2 = phate_operator.fit_transform(bmmsc_norm)

Calculating PHATE...
  Running PHATE on 2414 observations and 10738 variables.
  Calculating graph and diffusion operator...
    Calculating PCA...
    Calculated PCA in 2.14 seconds.
    Calculating KNN search...
    Calculated KNN search in 0.20 seconds.
    Calculating affinities...
    Calculated affinities in 0.04 seconds.
  Calculated graph and diffusion operator in 2.41 seconds.
  Calculating landmark operator...
    Calculating SVD...
    Calculated SVD in 0.14 seconds.
    Calculating KMeans...
    Calculated KMeans in 0.99 seconds.
  Calculated landmark operator in 1.58 seconds.
  Calculating optimal t...
    Automatically selected t = 17
  Calculated optimal t in 0.87 seconds.
  Calculating diffusion potential...
  Calculated diffusion potential in 0.21 seconds.
  Calculating metric MDS...
  Calculated metric MDS in 2.47 seconds.
Calculated PHATE in 7.55 seconds.

Check

1scprep.plot.scatter2d(Y_phate2, figsize=(12,8), ticks=False, label_prefix="PHATE")

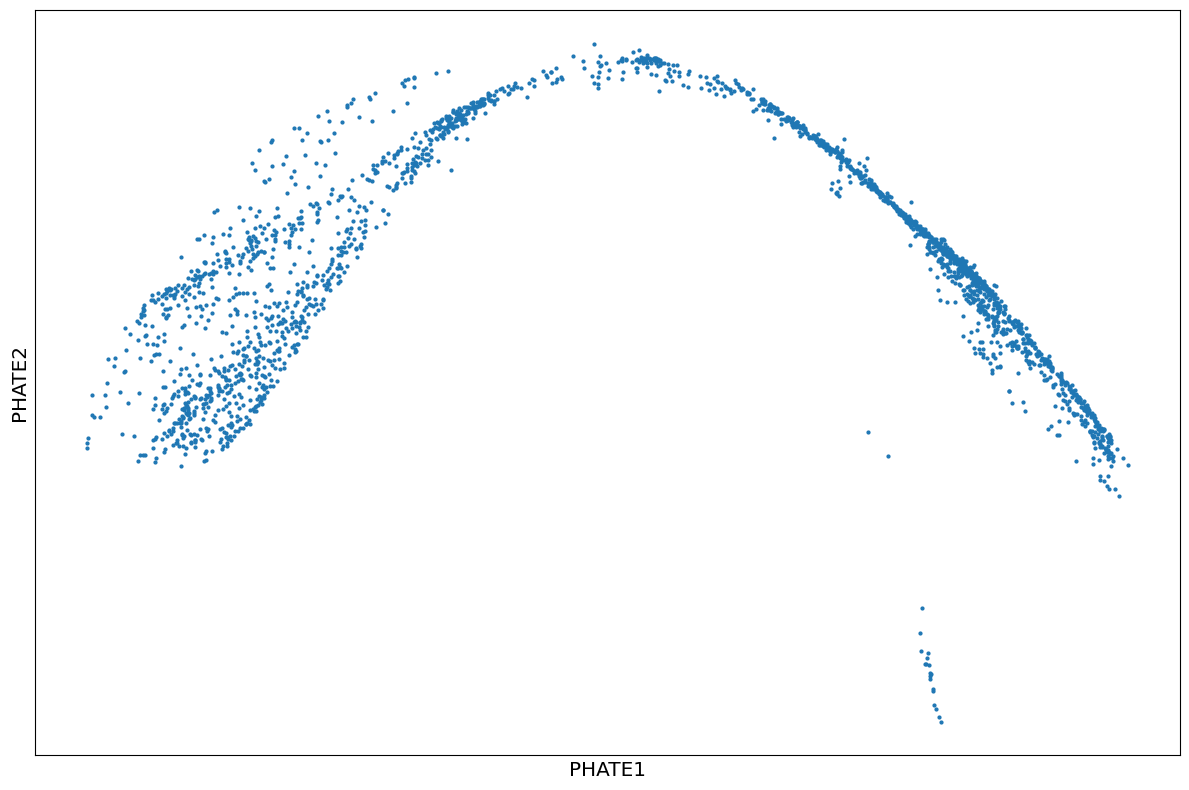
1phate_operator = phate.PHATE(knn=4, decay=100, t=10, n_jobs=-2)
2Y_phate3 = phate_operator.fit_transform(bmmsc_norm)
3scprep.plot.scatter2d(Y_phate3, figsize=(12,8), ticks=False, label_prefix="PHATE")

Calculating PHATE...
  Running PHATE on 2414 observations and 10738 variables.
  Calculating graph and diffusion operator...
    Calculating PCA...
    Calculated PCA in 2.31 seconds.
    Calculating KNN search...
    Calculated KNN search in 0.18 seconds.
    Calculating affinities...
  Calculated graph and diffusion operator in 2.53 seconds.
  Calculating landmark operator...
    Calculating SVD...
    Calculated SVD in 0.08 seconds.
    Calculating KMeans...
    Calculated KMeans in 1.21 seconds.
  Calculated landmark operator in 1.75 seconds.
  Calculating diffusion potential...
  Calculated diffusion potential in 0.15 seconds.
  Calculating metric MDS...
  Calculated metric MDS in 2.59 seconds.
Calculated PHATE in 7.02 seconds.

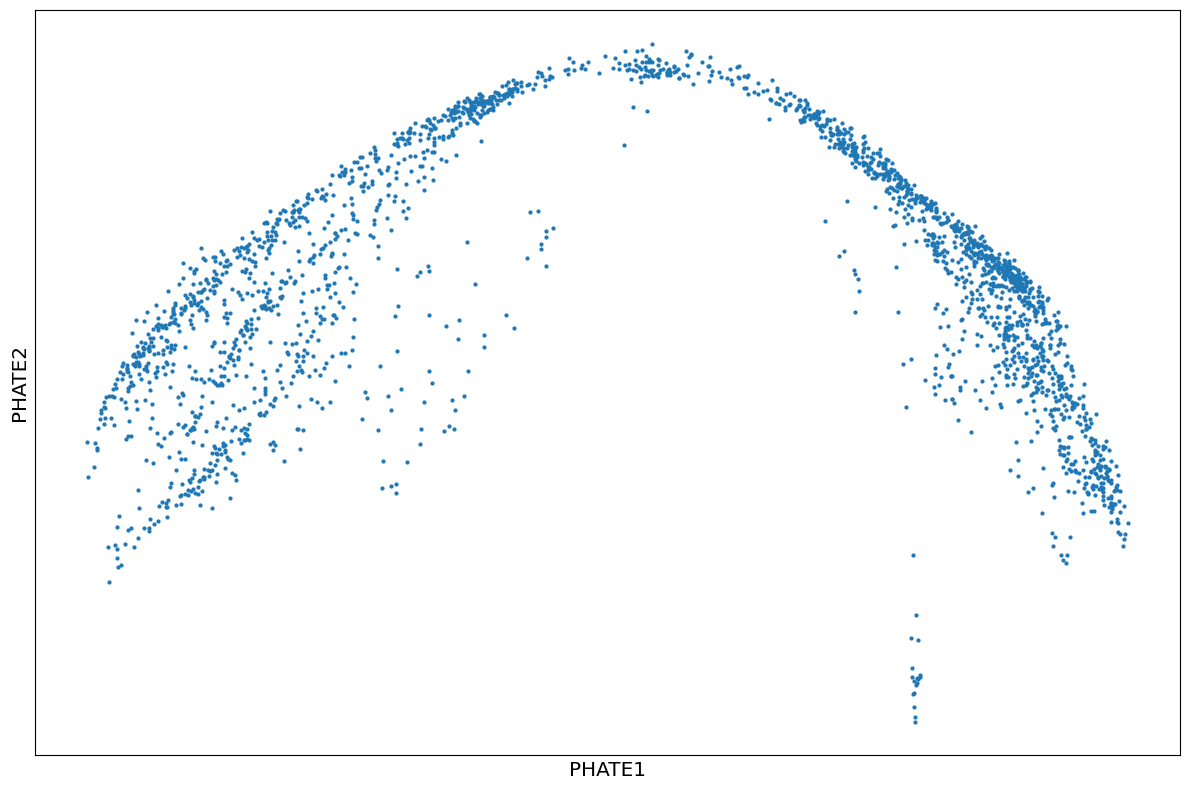
Set operator for 3D PHATE

1phate_operator.set_params(n_components=3)

PHATE(decay=100, knn=4, n_components=3, n_jobs=-2, t=10)

PHATE 3D

1Y_phate4 = phate_operator.fit_transform(bmmsc_norm)

Calculating PHATE...
  Running PHATE on 2414 observations and 10738 variables.
  Calculating graph and diffusion operator...
    Calculating PCA...
    Calculated PCA in 2.43 seconds.
    Calculating KNN search...
    Calculated KNN search in 0.20 seconds.
    Calculating affinities...
  Calculated graph and diffusion operator in 2.68 seconds.
  Calculating landmark operator...
    Calculating SVD...
    Calculated SVD in 0.12 seconds.
    Calculating KMeans...
    Calculated KMeans in 1.20 seconds.
  Calculated landmark operator in 1.77 seconds.
  Calculating diffusion potential...
  Calculated diffusion potential in 0.16 seconds.
  Calculating metric MDS...
  Calculated metric MDS in 14.05 seconds.
Calculated PHATE in 18.66 seconds.

3D interactive plotly using Mpo gene to label myeloid cells

 1df3 = pd.DataFrame(Y_phate4, columns=['x', 'y', 'z'])
 2df3['Mpo'] = bmmsc_norm['Mpo'].values
 3fig = px.scatter_3d(
 4    df3, 
 5    x='x', 
 6    y='y', 
 7    z='z',
 8    color='Mpo',
 9    color_continuous_scale="Plasma",
10    
11)
12
13fig.update_traces(marker=dict(size=2))
14
15fig.update_layout(
16    legend=dict(
17        itemsizing='constant',
18        font=dict(size=12)
19    ),
20    scene=dict(
21        xaxis=dict(
22            title='PHATE 1',
23            showticklabels=False,
24            showline=True,
25            zeroline=False,
26            linecolor='black',
27            backgroundcolor='rgba(0,0,0,0)',
28            gridcolor='lightgrey',
29            showgrid=True 
30        ),
31        yaxis=dict(
32            title='PHATE 2',
33            showticklabels=False,
34            showline=True,
35            zeroline=False,
36            linecolor='black',
37            backgroundcolor='rgba(0,0,0,0)',
38            gridcolor='lightgrey',
39            showgrid=True
40        ),
41        zaxis=dict(
42            title='PHATE 3',
43            showticklabels=False,
44            showline=True,
45            zeroline=False,
46            linecolor='black',
47            backgroundcolor='rgba(0,0,0,0)',
48            gridcolor='lightgrey',
49            showgrid=True
50        )
51    )
52)
53fig.write_html("../../../static/images/plot4.html", include_plotlyjs="embed")

Click here to view the interactive plot

Inspired by the tree PHATE examples I decided to use a similar approach here.

1phate_operator = phate.PHATE(knn=4, decay=100, t=120, n_jobs=-2, gamma = 0)
2Y_phate_tree = phate_operator.fit_transform(bmmsc_norm)

Calculating PHATE...
  Running PHATE on 2414 observations and 10738 variables.
  Calculating graph and diffusion operator...
    Calculating PCA...
    Calculated PCA in 2.12 seconds.
    Calculating KNN search...
    Calculated KNN search in 0.19 seconds.
    Calculating affinities...
  Calculated graph and diffusion operator in 2.35 seconds.
  Calculating landmark operator...
    Calculating SVD...
    Calculated SVD in 0.09 seconds.
    Calculating KMeans...
    Calculated KMeans in 1.38 seconds.
  Calculated landmark operator in 1.91 seconds.
  Calculating diffusion potential...
  Calculated diffusion potential in 0.31 seconds.
  Calculating metric MDS...
  Calculated metric MDS in 2.49 seconds.
Calculated PHATE in 7.07 seconds.

1phate.plot.scatter2d(Y_phate_tree, figsize=(8,6))

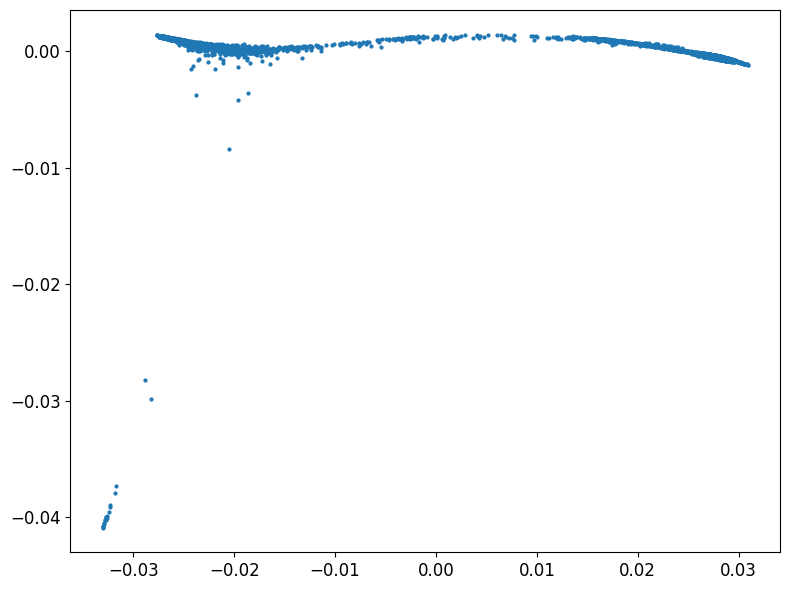
but it did not work very well.

Use scanpy to create an AnnData object and visualize the data with UMAP.

1cdata = ad.AnnData(
2    X=sp.csr_matrix(bmmsc.values)
3)

Qc preprocessing

 1sc.pp.calculate_qc_metrics(
 2    cdata, inplace=True, log1p=True
 3)
 4
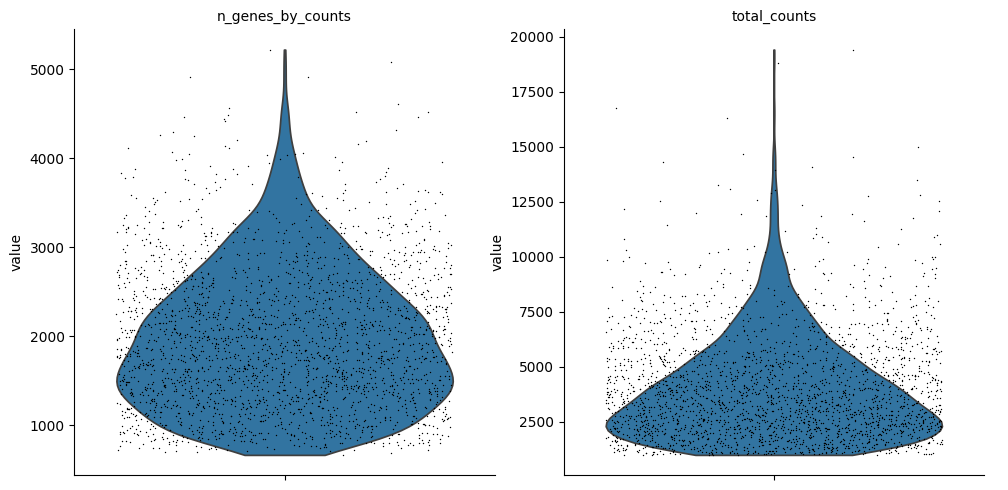
 5sc.pl.violin(
 6    cdata,
 7    ["n_genes_by_counts", "total_counts"],
 8    jitter=0.4,
 9    multi_panel=True,
10)

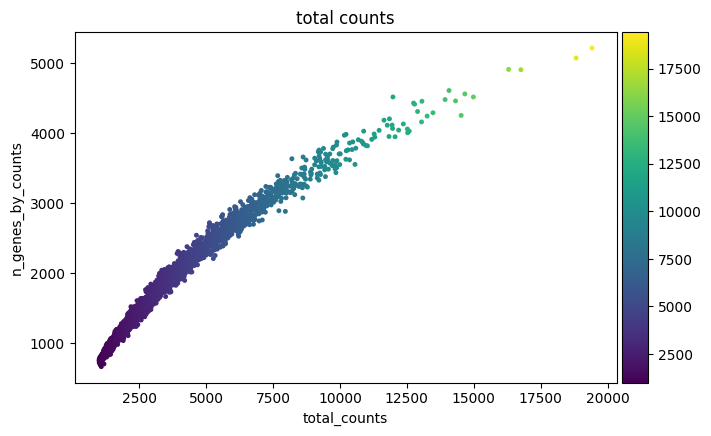
1sc.pl.scatter(cdata, "total_counts", "n_genes_by_counts", color="total_counts")

gene and cell filtering

1sc.pp.filter_cells(cdata, min_genes=100)
2sc.pp.filter_genes(cdata, min_cells=3)

Normalization

1# Saving count data
2cdata.layers["counts"] = cdata.X.copy()
3# Normalizing to median total counts
4sc.pp.normalize_total(cdata)
5# Logarithmize the data
6sc.pp.log1p(cdata)

Highly variable genes and PCA

1sc.pp.highly_variable_genes(cdata, n_top_genes=2000)
2sc.tl.pca(cdata)

Neighbors and UMAP

1sc.pp.neighbors(cdata)
2sc.tl.umap(cdata)
3sc.pl.umap(cdata)

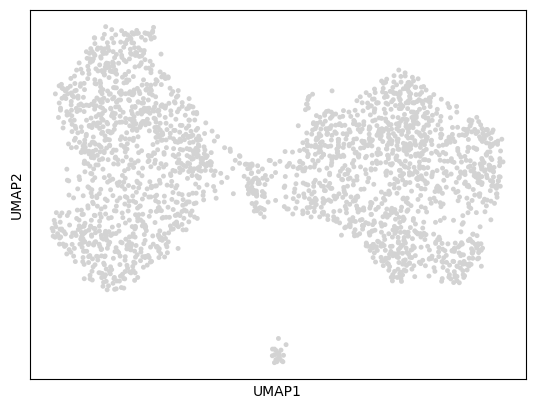
3D UMAP

1sc.tl.umap(cdata, n_components=3, key_added='UMAP_3D')

Interactive plotly colorinbg by Mpo gene

 1df4 = pd.DataFrame(cdata.obsm['UMAP_3D'], columns=['x', 'y', 'z'])
 2df4['Mpo'] = bmmsc_norm['Mpo'].values
 3fig = px.scatter_3d(
 4    df4, 
 5    x='x', 
 6    y='y', 
 7    z='z',
 8    color='Mpo',
 9    color_continuous_scale="Plasma",
10    
11)
12
13fig.update_traces(marker=dict(size=2))
14
15fig.update_layout(
16    legend=dict(
17        itemsizing='constant',
18        font=dict(size=12)
19    ),
20    scene=dict(
21        xaxis=dict(
22            title='UMAP 1',
23            showticklabels=False,
24            showline=True,
25            zeroline=False,
26            linecolor='black',
27            backgroundcolor='rgba(0,0,0,0)',
28            gridcolor='lightgrey',
29            showgrid=True 
30        ),
31        yaxis=dict(
32            title='UMAP 2',
33            showticklabels=False,
34            showline=True,
35            zeroline=False,
36            linecolor='black',
37            backgroundcolor='rgba(0,0,0,0)',
38            gridcolor='lightgrey',
39            showgrid=True
40        ),
41        zaxis=dict(
42            title='UMAP 3',
43            showticklabels=False,
44            showline=True,
45            zeroline=False,
46            linecolor='black',
47            backgroundcolor='rgba(0,0,0,0)',
48            gridcolor='lightgrey',
49            showgrid=True
50        )
51    )
52)
53fig.write_html("../../../static/images/plot5.html", include_plotlyjs="embed")

Click here to view the interactive plot

As in the EB dataset, PHATE and UMAP look different but the biological relationships stay the same both in 2D and 3D.

Pancreas Data set

I read the data from the same object as in the slingshot post, but this time using scanpy since we are working on Python.

1adata = sc.read('../2025-04-06-slingshot/endocrinogenesis_day15.h5ad')
2adata

AnnData object with n_obs × n_vars = 3696 × 27998
    obs: 'clusters_coarse', 'clusters', 'S_score', 'G2M_score'
    var: 'highly_variable_genes'
    uns: 'clusters_coarse_colors', 'clusters_colors', 'day_colors', 'neighbors', 'pca'
    obsm: 'X_pca', 'X_umap'
    layers: 'spliced', 'unspliced'
    obsp: 'distances', 'connectivities'

2D PHATE

1phate_operator = phate.PHATE(n_jobs=-2)
2pancreas_phate = phate_operator.fit_transform(adata.to_df())

Calculating PHATE...
  Running PHATE on 3696 observations and 27998 variables.
  Calculating graph and diffusion operator...
    Calculating PCA...
    Calculated PCA in 4.08 seconds.
    Calculating KNN search...
    Calculated KNN search in 0.32 seconds.
    Calculating affinities...
    Calculated affinities in 0.03 seconds.
  Calculated graph and diffusion operator in 4.51 seconds.
  Calculating landmark operator...
    Calculating SVD...
    Calculated SVD in 0.21 seconds.
    Calculating KMeans...
    Calculated KMeans in 2.07 seconds.
  Calculated landmark operator in 2.80 seconds.
  Calculating optimal t...
    Automatically selected t = 23
  Calculated optimal t in 1.59 seconds.
  Calculating diffusion potential...
  Calculated diffusion potential in 0.41 seconds.
  Calculating metric MDS...
  Calculated metric MDS in 3.35 seconds.
Calculated PHATE in 12.66 seconds.

Plot coloring by cell type

1phate.plot.scatter2d(pancreas_phate, c=adata.obs['clusters'], figsize=(8,6))

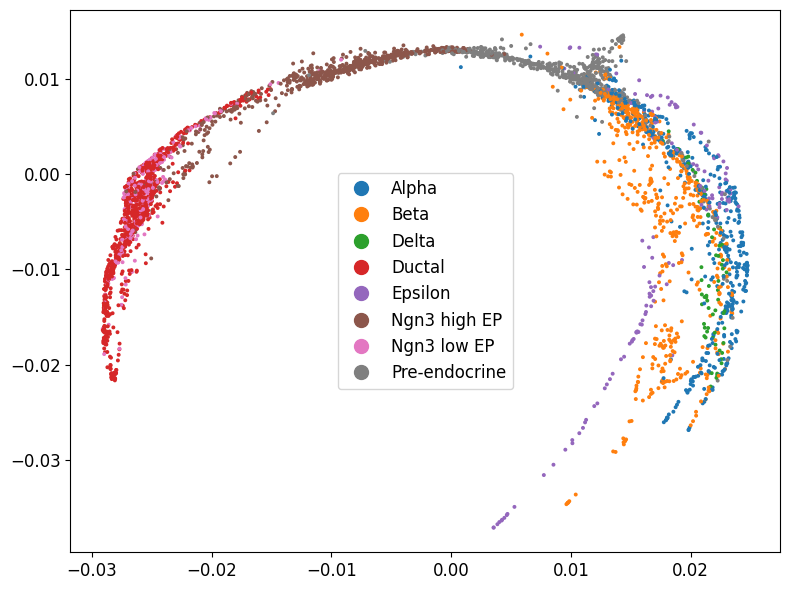
add PHATE coordinates to adata object

1adata.obsm['phate'] = pancreas_phate

plot using scanpy to get the same color scheme as in the next UMAP plot

1sc.pl.embedding(adata, 'phate', color = 'clusters')

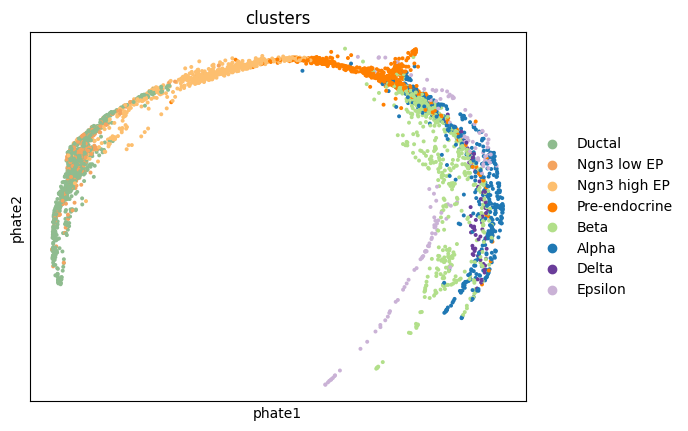
try different PHATE settings

1phate_operator = phate.PHATE(n_jobs=-2, knn=4, decay=100, t=10)
2pancreas_phate = phate_operator.fit_transform(adata.to_df())

Calculating PHATE...
  Running PHATE on 3696 observations and 27998 variables.
  Calculating graph and diffusion operator...
    Calculating PCA...
    Calculated PCA in 3.12 seconds.
    Calculating KNN search...
    Calculated KNN search in 0.34 seconds.
    Calculating affinities...
    Calculated affinities in 0.02 seconds.
  Calculated graph and diffusion operator in 3.54 seconds.
  Calculating landmark operator...
    Calculating SVD...
    Calculated SVD in 0.13 seconds.
    Calculating KMeans...
    Calculated KMeans in 1.31 seconds.
  Calculated landmark operator in 1.97 seconds.
  Calculating diffusion potential...
  Calculated diffusion potential in 0.22 seconds.
  Calculating metric MDS...
  Calculated metric MDS in 3.51 seconds.
Calculated PHATE in 9.24 seconds.

1adata.obsm['phate2'] = pancreas_phate
2sc.pl.embedding(adata, 'phate2', color = 'clusters')

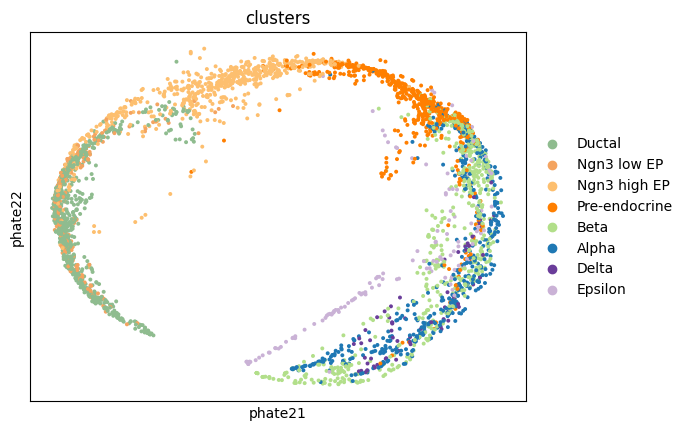
Plot UMAP

1sc.pl.umap(adata, color = 'clusters')

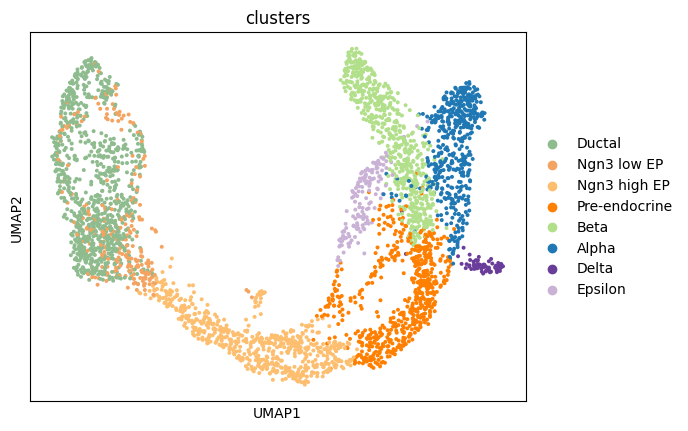
In this case, UMAP looks better with more clearly separated cell types.

Conclusions

The PHATE seems to be working better, with default settings, is some datasets but worse in others.
In general, UMAP seems to provide similar biological conclusions as PHATE, but the visualizations are different.
As seen in my previous post for t-SNE and UMAP, parameters choice has a big impact on the results.

Take away

t-SNE are directly integrated in SCE, Seurat and Scanpy so it is easy to use them.
PHATE works natively in Python and, using reticulate, in R.
I will start with t-SNE/UMAP representations and move to PHATE if I am not happy with the results.

Single Cell Dimensional Reduction: Phate

Embriod Body differentiation

Bone Marrow

Pancreas Data set

Conclusions

Take away

Further reading